fisica experimental erro absoluto

Errores Absolutos y Relativos

Compartir en..., síguenos en..., errores en la medición.

Lo creas o no, cada vez que medimos tenemos una gran probabilidad de cometer algún tipo de error que nos ofrezca un resultado mas o menos alejado del que realmente deberíamos obtener. Y es que medir, es más bien un proceso aproximado que exacto. De entre los errores más comunes podemos distinguir dos grandes grupos:

• Error de calibrado . Se trata de uno de los errores más frecuentes y está ligado directamente al instrumento. Muchos de ellos deben ser configurados de forma apropiada antes de ser utilizados (calibrado), si esto no se hace correctamente todas las medidas realizadas tendrán añadidas un sesgo.
• Error de paralaje . Es propio de instrumentos de medida analógicos como por ejemplo aquellos que poseen agujas para marcar los valores. Dos observadores situados en posiciones oblicuas a la aguja pueden leer valores diferentes.
• Errores aleatorios o accidentales . Se tratan de errores que se producen debido a causas que no se pueden controlar. Para intentar reducir el efecto de este tipo de errores se suele medir varias veces en las mismas condiciones y se considera como valor final más probable la media aritmética de los datos obtenidos.

Dado que todas las medidas están afectadas por un error experimental, en el mundo científico es común hacer constar cada resultado obtenido en una medición junto con la incertidumbre sobre esa medida. La incertidumbre es un valor numérico que se obtiene por medio de dos nuevos conceptos denominados error absoluto y error relativo.  

Medición científica

Cada resultado de una medición viene dado por el valor númerico de la medición acompañado de un valor de incertidumbre sobre la medida.

A continuación vamos a estudiar como calcular estos dos tipos de error. ¿Estás preparado?.

Error absoluto

El error absoluto de una medida ( ε a ) es la diferencia entre el valor real de la medida ( X ) y el valor que se ha obtenido en la medición ( X i ). 

ε a = X - X i

El error absoluto puede ser un valor positivo o negativo, según si la medida es superior al valor real o inferior y además tiene las mismas unidades que las de la medida.

Cálculo del error absoluto

Para calcular el error absoluto de una medida es imprescindible conocer en primer lugar qué valor se considera como real. Por norma general ese valor es la media de los valores obtenidos al realizar un número n de mediciones en las mismas condiciones.

Con el fin de facilitar su cálculo cada uno de los valores obtenidos tras cada medición (X i ) se suelen escribir en una tabla junto con las veces que se produce a lo largo de todas las mediciones (f i ). Por ejemplo, imagina que pesamos 20 veces un mismo objeto (n = 20). Para representar los valores obtenidos se suele realizar una tabla como la siguiente:

Esta tabla muestra que al medir hemos obtenido el valor 3.45 g 2 veces, 3.40 g 3 veces, 3.52 g 5 veces, etc...

A continuación le añadimos una columna que muestra la multiplicación de la medida por la frecuencia de cada fila , incluyendo al final la suma de los valores de esta nueva columna:

La media de las medidas obtenidas ( X ) será este valor X i ·f i dividido por el número de medidas que hicimos ( n = 20 ):

X = ∑ i = 1 n X i · f i n = ∑ i = 1 20   X i · f i 20 = 69 . 75 20 = 3 . 4875

Como hemos comentado anteriormente, esta media que hemos calculado es el valor que consideraremos como real . Dado que el error absoluto ( ε a ) de cada medida es la diferencia entre el valor real  y el valor obtenido en la medición, vamos a añadir una nueva columna en la que se restan ambos valores:

De esta forma tenemos representados en la tabla todos los errores absolutos de cada uno de los valores de las medidas que hemos realizado.

Imprecisión absoluta

Una vez que hemos calculado el error absoluto de cada una de las medidas obtenidas, podemos calcular lo que se denomina imprecisión absoluta. La imprecisión absoluta se puede considerar como el error absoluto del conjunto de medidas que hemos realizado. Mas concretamente:

La imprecisión absoluta (Ea) es la media de los errores absolutos tomados con signos positivos:

E a = ∑ i = 1 n X - X i n

En el ejemplo que nos ocupa:

E a = ∑ i = 1 20 X - X i n = 0 . 1925 20 = 0 . 009625   g

¿Para qué sirve el error absoluto?

El error absoluto es un indicador de la imprecisión que tiene una determinada media. De hecho, cuando se proporciona el resultado de una medida suele venir acompañada de dicha imprecisión.

Ejemplo: Imagina que al medir un determinado objeto con un instrumento de precisión ± 1 cm obtenemos el valor de 23.5 cm. Si adicionalmente sabemos que la imprecisión absoluta de esa medida es 0.2 cm, entonces el resultado de esa medición se representa como: 23.5 cm ± 0.2 cm donde el valor real de la magnitud queda incluida en el intervalo 23.3 cm <= 23.5 cm <= 23.7 cm.

De forma general:

1. Si únicamente realizamos una sola medición con el instrumento de medida, el resultado final será el valor leído ± la precisión del instrumento de medida.

2. Si realizamos n medidas en las mismas condiciones, tomaremos como valor la media aritmética (X) ± el menor valor entre la imprecisión absoluta y la precisión del instrumento de medida.

Se realiza un experimento que consiste en medir el tiempo en el que tarda en llegar al suelo una bola que se deja caer desde una determinada altura. Para ello se utiliza un cronómetro cuya precisión es de 0.1 s. Las medidas obtenidas tras repetir el experimento son: 3.1, 3.2, 3.7, 3.4, 3.5, 3.4, 3.1, 3.4, 3.5, 3.9. Determina científicamente el resultado obtenido. 

Error relativo

Es el cociente entre el error absoluto y el valor que consideramos como exacto (la media). Al igual que el error absoluto puede ser positivo o negativo porque puede se puede producir por exceso o por defecto y al contrario que él no viene acompañado de unidades. 

ε r = ε a X

De igual forma, se puede multiplicar por 100 obteniéndose así el tanto por ciento (%) de error.

ε r = ε a X · 100   %

Como ejemplo podemos calcular el error relativo sobre nuestro ejemplo.  De esta forma obtenemos que:

ε r = 9 . 625 · 10 - 3 3 . 4875 · 100   % = 0 . 27   %

¿Para qué sirve el error relativo?

El error relativo tiene la misión de servir de indicador de la calidad de una medida. Para entender este concepto utilizaremos otro ejemplo. Imagina que se comete un error absoluto de 1 metro al medir una finca de 200 metros y otra de 3000. Si calculamos los errores relativos en ambas mediciones tenemos que son 1/200 y 1/3000. Dado que en la segunda medición el error relativo es más pequeño quiere decir que la calidad de la medida es mucho mejor que la de la primera. De hecho si lo piensas, bien es mucho mejor equivocarse en un metro cuando cuento 3000 metros que cuando cuento 200 metros.

Cuando se realizan una medición se considera que su calidad es mucho mayor cuanto más pequeño es el error relativo que se comete.

Y ahora... ¡Ponte a prueba!

José L. Fernández

Apartados relacionados.

Este mismo apartado se encuentra desarrollado en otros niveles educativos. Si sus contenidos no se ajustan al nivel que buscas, prueba a visitar:

Por otro lado, los contenidos de Errores Absolutos y Relativos se encuentran estrechamente relacionados con:

Error absoluto y error relativo: Qué son y cómo se calculan

Los errores absolutos y relativos son dos tipos de errores experimentales ¿Cuál es la diferencia entre ellos y cómo se calculan?

Es lo que vamos a ver a continuación, pero antes, tenemos que aprender un poco más sobre los errores en las medidas.

Si has llegado hasta aquí es porque buscas ayuda para resolver algún problema de física y necesitas clases de física online y es muy probable que también necesites refuerzo en matemáticas . Si después de leer esto, quieres seguir aprendiendo paso a paso, en una plataforma donde tengas todo explicado, con ejercicios resueltos y alguien que te resuelva tus dudas, solo tienes que apuntarte a los Cursos de Física Online :

VER CURSOS DE FÍSICA ONLINE

Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas y física . Puedo explicarte paso a paso cualquier duda que no entiendas.

Sólo tienes que dejarte guiar y verás como vas a aprendiendo poco a poco a resolver tus problemas de física

En este vídeo tienes explicados cómo calcular el error absoluto y el error relativo con ejercicios resueltos paso a paso:

https://youtu.be/FB8FWO8ze0o

Y a continuación tienes todo explicado más despacio:

Índice de Contenidos

Error en las medidas

En cualquier medición que se realice, siempre se cometen errores. Estos errores pueden provenir de dos fuentes: errores sistemáticos y los aleatorios o accidentales.

Los errores sistemáticos  son los debidos al aparato de medida y se pueden corregir utilizando instrumentos adecuados. Para que un aparato sea adecuado, tiene que se fiel, exacto y preciso:

• Un aparato es fiel cuando al medir el mismo objeto varias veces, el resultado es el mismo
• Un aparato es exacto cuando el resultado obtenido coincida con el valor real
• Un aparato es preciso cuando es capaz de medir pequeñas variaciones de una magnitud.

Los errores aleatorios o accidentales , son los debidos a la persona que está realizando la medición. Estos errores se dan por defecto y por exceso. Para reducirlos, se realizan repetidas mediciones y se utiliza como valor exacto el valor medio.

Por tanto, todas las medidas están afectadas por un error experimental y es por eso que la medición va acompañada por una incertidumbre , que es un valor que se obtiene gracias al cálculo del error absoluto y el error relativo :

Error absoluto

El error absoluto se define como la diferencia entre el valor real y el valor aproximado, en valor absoluto:

• El valor real es el valor que en teoría mide la magnitud a medir
• El valor aproximado es la media de las diferentes medidas

Este valor del error absoluto es el debido a la persona que realiza la medición. Además, está el error debido a la precisión del instrumento de medida, que coincide con la unidad más pequeña con la que puede medir el aparato.

El error absoluto será el mayor valor entre el error del medidor y el error del aparato.

El error absoluto se mide en las mismas unidades que la medición.

Además, se expresa siempre con una cifra distinta de cero, redondeándose siempre en exceso. Es decir, no podemos expresar el error absoluto de esta forma:

Sino que el 0,018 debemos redondearlo a 0,02:

Por otro lado, error no puede ser más precisa (en decimales) que el error. Deben ser igual de precisas . Si el error está expresado en centésimas, la medición no puede ir expresada en unidades:

Sino que la medición debe ir también expresada en centésimas:

Si la medición es un número entero, entonces para llegar a las centésimas añadiríamos ceros después de la coma.

Ejemplo de cálculo de error absoluto

Una barra de metal mide 10 metros de largo. La medimos con un metro calibrado en milímetros y nos da una medición de 9,998 metros. ¿Cuál es el error absoluto?

En nuestro caso, el metro mide en milímetros, luego el error del aparato es:

El error debido a la persona que realiza la medición es la diferencia entre el valor real y el valor aproximado:

En este caso el valor es 10 m y el valor aproximado es 9,998 m, que es el valor obtenido, por lo que el error es:

Una vez obtenidos el error del aparato y el error del medidor, el error absoluto es el mayor de los dos:

Observa como tanto la medida como el error están expresados en milésimas y el error sólo tiene una cifra distinta de cero.

Cálculo del error absoluto en medidas directas

Vamos a ver ahora cómo calcular el error absoluto cuando se realizan varias medidas directas .

En este caso debemos utilizar la siguiente fórmula:

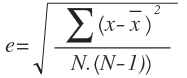
Donde en el numerador tenemos la suma del cuadrado de cada dato medido menos el valor medio de los datos  y en el denominador N es el número de datos.

Por ejemplo:

En un experimento tomamos las siguientes medidas de tiempo. ¿Cuál es el error absoluto de la medida?:

En primer lugar, calculamos la media de las mediciones, que será el valor exacto de la medición . Para ello, sumamos todos los valores y dividiendo entre el número de mediciones, que en este caso es 5:

Calculamos y nos queda:

Por tanto, este valor de 17,242 s, lo consideraremos el valor exacto de la medición.

Vamos a calcular el error absoluto de la medición aplicando la siguiente fórmula:

Empezamos calculando la suma del numerador. Para ello, añadimos una columna a la tabla de datos, donde a cada valor le restaremos la media:

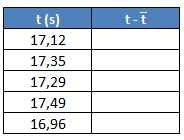
Por ejemplo, para el primer dato de 17,12 s, este cálculo nos queda:

Lo hacemos igual para el resto de valores y lo vamos escribiendo en esta columna:

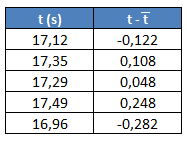
Después añadimos otra columna donde elevamos los valores obtenidos en la segunda columna al cuadrado:

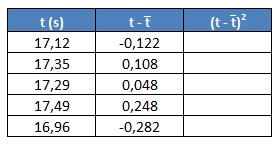
Por ejemplo, para el primer valor de la segunda columna sería:

Lo hacemos igual para el resto de datos:

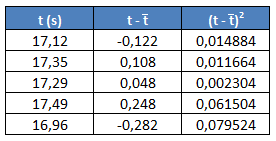
Estamos buscando la suma del valor de cada dato menos la media al cuadrado, por tanto, para obtenerlo, sólo tenemos que sumar todos los valores de la tercera columna:

Sustituimos este valor en la fórmula, N lo sustituimos por 5, que es el número de datos que tenemos y calculamos:

Este error absoluto corresponde al error del medidor:

El valor del error absoluto debe tener sólo una cifra distinta de cero y reondearse por exceso, por lo que redondeamos a 0,1:

Por otro lado, debemos obtener el error del aparato , que es igual a la unidad más pequeña con la que puede medir el instrumento de medida. En nuestro caso el error del aparato es 0,01, ya que hemos podido medir hasta centésimas de segundo:

El error absoluto es el mayor entre el error del medidor y el error del aparto. Como el mayor es el error del medidor nos quedamos con el valor de 0,1 s para el error absoluto.

La medida final la expresamos como el valor exacto, que era la media de las medidas con su error absoluto:

Como el valor de la medición y el error deben tener la misma precisión (mismo número de decimales), ajustamos el valor exacto a los decimales del error, por lo que nos queda que el valor final de la medición es:

Error relativo

El error relativo se calcula dividiendo el error absoluto entre el valor exacto:

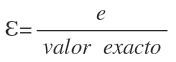
El error relativo se mide en porcentaje, luego para obtener directamente el error en tanto por ciento, a la expresión anterior hay que multiplicarla por 100:

El error relativo lo utilizamos para determinar la precisión de la medición. Nos dice la proporción del error con respecto al valor exacto de la medición. Una medida es buena cuando no supera el 5%.

Ejemplo de error relativo

Vamos a ver un ejemplo de cálculo de error relativo:

Queremos medir 180 cm³ de agua con una probeta con un error relativo menor del 3%. ¿Bastará con una probeta graduada de 5 en 5 cm³ o necesitaremos una que vaya de 2 en 2 cm³?

El valor exacto de la medida es 180 cm³. Con la probeta graduada de 5 en 5 cm³, tenemos un error del aparato de 5 cm³, que es el error absoluto de la medición en este caso, por lo que la medida con su error nos queda:

Vamos a calcular el error relativo para este caso con la fórmula:

Sustituimos el error absoluto y el valor exacto y calculamos:

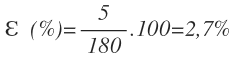
El valor relativo que obtenemos es de 2,7%, que es menor de 3%, por lo que la probeta graduada de 5 en 5 cm³ nos valdría.

Vamos a ver el caso de la probeta graduada de 2 en 2 cm³. En este caso la medida con su error absoluto es:

Calculamos su error relativo:

El error relativo es todavía más bajo que en el caso anterior, ya que tenemos más precisión en la medida.

Por tanto, cualquiera de las dos probetas nos valdría y con la segunda obtenemos una mayor precisión.

Cálculo del error absoluto en medidas indirectas

Veamos cómo calcular el error absoluto cuando las medidas con indirectas , es decir, se obtienen haciendo operaciones a partir de otras medidas tomadas directamente.

Se distinguen dos casos:

• Cuando en la expresión matemática sólo aparecen sumas y restas , el error absoluto es la suma de los errores absolutos de las medidas directas.
• Cuando en la expresión matemática aparecen productos, divisiones y potencias , el error relativo del producto es la suma de los errores relativos de las diferentes magnitudes implicadas, multiplicadas por sus exponentes .

Vamos a ver un ejemplo de cada uno de los casos.

Cómo calcular el error absoluto en medidas indirectas cuando sólo aparecen sumas y rectas

Calcular el perímetro del siguiente rectángulo:

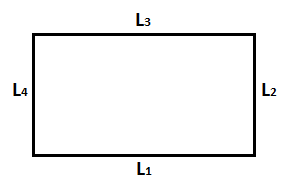
Sabiendo que las medidas de sus lados son:

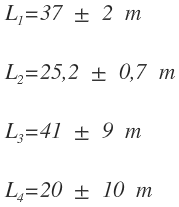
El perímetro de este rectángulo es:

Para calcular el valor exacto del perímetro sumamos los valores de las medidas:

Para calcular el error absoluto del perímetro, sumamos los valores de los errores absolutos:

El error absoluto sólo puede tener una cifra distinta de cero, por lo que redondeamos por exceso:

El valor del perímetro con su error es:

Como la medida y el error deben tener la misma precisión, ajustamos el número de decimales del valor de la medida al número de decimales del error (ninguno) y redondeamos (en este caso no es necesario que sea siempre por exceso).

El valor de final del perímetro es:

Cómo calcular el error absoluto en medidas indirectas cuando aparecen productos, divisiones y potencias

Supongamos que queremos calcular el valor de M junto con su error y que M se calcular mediante la siguiente expresión:

Los valores de l y de t son:

En primer lugar calculamos M con los valores exactos de l y t:

Ahora vamos a calcular el error absoluto de M. Como en la expresión para calcular M aparecen productos, sabemos que el error relativo de M es igual al error relativo de l, multiplicado por su exponente, más el error relativo de l multiplicado por su exponente:

Por otro lado, sabemos que el error relativo es igual al error absoluto dividido por el valor exacto:

Sustituimos esta última expresión en cada uno de los errores relativos. En el caso del error relativo de M, no conocemos su valor absoluto, puesto que es lo que queremos calcular, y lo dejamos como incógnita:

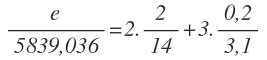
Operamos en el segundo miembro:

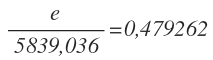
Pasamos el denominador del primer miembro multiplicando al segundo miembro y calculamos:

Redondeamos el error absoluto por exceso:

El valor de M con su error es:

Finalmente, ajustamos el número de decimales del valor de la medida al número de decimales del error y redondeamos:

Vamos a ver otro ejemplo de cómo calcular el error absoluto en medidas indirectas :

Tres estudiantes determinan el volumen de un mismo cilindro. El primero lo hace directamente y obtiene una medida de 308 ± 4 cm³. El segundo lo hace midiendo el diámetro de la base y la altura con una regla y después calculando el volumen con la fórmula V=(π.D².h)/4. Las medidas que obtiene son h=12,5 ± 0,1 cm y D=5,6 ± 0,1 cm. El tercero también utiliza la fórmula del volumen pero utiliza un calibre para tomar medidas. Las medidas que obtiene son h=12,54 ± 0,01 cm y D=5,62 ± 0,01 cm. Hallar los tres volúmenes.

El volumen del primer alumno ya lo tenemos puesto lo obtiene directamente:

El segundo alumno obtiene las siguientes medidas:

Utiliza la siguiente fórmula para calcular el volumen:

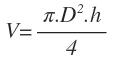
Para poder utilizar la expresión de los errores relativos, es necesario que tengamos un producto de factores. Para ello, en vez de dividir entre 4, lo que hacemos es convertir el denominador en la fracción 1/4, que multiplique al resto de factores:

Calculamos el valor exacto de V con los valores de las medidas de h y de D:

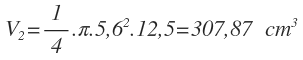
El error absoluto lo calculamos a partir de los errores relativos. El error relativo del volumen será igual a la suma de los errores relativos de cada uno de los factores, multiplicados por su exponente:

El error relativo de 1/4 y el error relativo de π se consideran despreciables y por tanto son igual a 0. El resto de errores relativos los sustituimos por los errores absolutos entre el valor exacto, quedando como incógnita el error absoluto del volumen:

Redondeamos el valor del error absoluto por exceso:

La medida del volumen del segundo alumno con su error es:

Finalmente redondeamos el valor de la medida para que tenga la misma precisión que el error:

El tercer alumno obtiene las siguientes medidas:

Utilizamos la siguiente fórmula para calcular el volumen:

Sustituimos valores y calculamos el valor exacto del volumen:

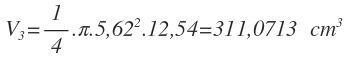
Igual que antes, utilizamos los errores relativos para calcular el error absoluto:

Sustituimos los errores relativos por el error absoluto entre el valor exacto:

Y pasamos el denominador del primer miembro multiplicando al segundo miembro:

El valor del volumen con su error es:

Finalmente, redondeamos el valor exacto para que tenga la misma precisión que el error:

¿Necesitas ayuda en física y matemáticas? ¿Quieres que te explique cualquier duda que te surja?

Puedo enseñarte exactamente lo que necesitas aprender para entender física y las matemáticas que necesitas aplicar .

He diseñado un método práctico y efectivo que te ayudará a entender la física así como las matemáticas que necesitas aplicar , paso a paso, explicándote justo lo que necesitas para saber resolver todos problemas y saber aplicar las fórmulas que correspondan. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.

Con mi método:

• Sabrás los pasos exactos que tienes que dar para resolver tus problemas de física
• Conseguirás resultados en muy poco tiempo , sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión

Suena bien ¿no?

¿Por qué tardar 2 horas buscando información por Internet si puedes aprenderlo en menos de 20 minutos ?

Te explicaré lo que necesitas aprender para entender física y las matemáticas que necesitas aplicar. ¿Quieres informarte de como puedes aprender física y matemáticas? Pulsa el botón para saber más:

ENSÉÑAME FÍSICA

Errores absolutos y relativos

En este post te explicamos qué son el error absoluto y el error relativo y cuál es la diferencia entre estos dos tipos de errores. También encontrarás cómo calcular el error absoluto y el error relativo, un ejercicio resuelto y, además, podrás hallar el error absoluto y el error relativo de cualquier medición con una calculadora online.

Error absoluto

El error absoluto es la diferencia entre el valor real y el valor medido. Por lo tanto, para calcular el error absoluto de una medición se debe restar el valor real de la medida menos el valor obtenido de la medición.

De modo que la fórmula del error absoluto es la siguiente:

Fíjate que el error absoluto puede ser positivo o negativo, dependiendo de si el valor medido es respectivamente menor o mayor que el valor real de la medida.

Nota: el error absoluto de una medida también se puede definir como el valor absoluto de la diferencia entre el valor real y el valor medido. No obstante, se suele calcular sin el valor absoluto, ya que así también se sabe si el valor obtenido al hacer la medida es mayor o menor que el valor real.

Error relativo

El error relativo se define como el cociente entre el error absoluto y el valor exacto. Por lo tanto, para calcular el error relativo de una medición se debe restar el valor real menos el valor medido y luego dividir por el valor real.

Así pues, la fórmula del error relativo es la siguiente:

El error relativo también se puede expresar en forma de porcentaje (error relativo porcentual), para ello simplemente tenemos que multiplicar el error relativo por 100.

Ejemplo del cálculo de errores absolutos y relativos

Ahora que ya sabemos cuáles son las fórmulas del error absoluto y el error relativo, vamos a ver varios ejemplos de cómo se calculan este tipo de errores.

• Una empresa industrial que fabrica barras de acero procede a hacer un control de calidad. Para ello, produce una muestra de cinco barras que en teoría deben medir 3 m de longitud y mide sus longitudes reales, puedes ver los datos recopilados expresados en metros a continuación. Calcula los errores absolutos y relativos de las mediciones realizadas.

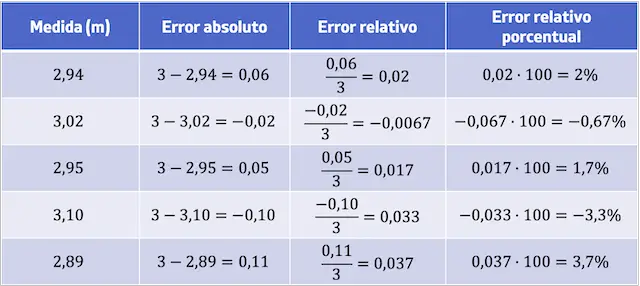
Por ejemplo, si el valor medido es 2,94 y el valor real es 3, el error absoluto es igual a 3-2,94=0,06. Por otro lado, para calcular el error relativo tenemos que dividir el error absoluto por el valor real, por lo tanto, en este caso el error relativo es 0,06/3=0,02 (expresado en forma de porcentaje es 2%).

Así pues, tenemos que hacer el mismo procedimiento para todos los datos. Puedes ver los resultados de los cálculos de todos los errores absolutos y relativos en la siguiente tabla:

Diferencia entre error absoluto y error relativo

Para acabar de entender los dos conceptos, vamos a ver en detalle cuál es la diferencia entre los errores absolutos y los errores relativos.

La diferencia entre el error absoluto y el error relativo es que el error absoluto indica la discrepancia absoluta entre el valor real y el valor medido, en cambio, el error relativo compara la diferencia entre el valor real y el valor medido con el valor real.

Por lo tanto, el error absoluto sirve para determinar cuánto de lejos está el valor medido del valor real, mientras que el valor relativo se usa para saber si el error cometido es muy grande o no en función del valor que tenga la medida real.

Por ejemplo, un error absoluto de 4 puede ser muy grande o muy pequeño, pues no es lo mismo cometer un error de 4 unidades si el valor real es 1000 o si es 10. En el primer caso, el error relativo es del 0,4%, pero en el segundo caso el error relativo es del 40%. De modo que el error cometido en el primer caso en realidad es mucho mayor que en el segundo caso.

Así pues, el error relativo nos permite identificar si realmente el error cometido en la medición es muy grande o no.

Calculadora de errores absolutos y relativos

Introduce el valor real y el valor medido en la siguiente calculadora y pulsa el botón de abajo para calcular el error absoluto y el error relativo de la medición:

Deja un comentario Cancelar respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Correo electrónico*

Error absoluto y error relativo

Como consecuencia de la existencia de diferentes fuentes de error, el científico se plantea por sistema hasta qué punto o en qué grado los resultados obtenidos son fiables, esto es, dignos de confianza. Por ello, al resultado de una medida se le asocia un valor complementario que indica la calidad de la medida o su grado de precisión. Los errores o imprecisiones en los resultados se expresan matemáticamente bajo dos formas que se denominan error absoluto y error relativo. Se define el error absoluto ΔE, como la diferencia entre el resultado de la medida M y el verdadero valor m₀ de la magnitud a medir

ΔE = M - m₀

El error relativo Eᵣ es el cociente entre el error absoluto ΔE y el verdadero valor. Cuando se expresa en tanto por ciento su expresión es

En sentido estricto tales definiciones son únicamente aplicables cuando se refieren no a medidas físicas propiamente, sino a operaciones matemáticas, ya que el valor exacto de una magnitud no es accesible. Por ello, con frecuencia se prefiere hablar de incertidumbres en lugar de errores. En tal caso se toma como m el valor que más se aproxima al verdadero, es decir, valor medio obtenido al repetir varias veces la misma medida.

Cifras significativas

Los científicos procuran que sus datos experimentales no digan más de lo que pueden decir según las condiciones de medida en los que fueron obtenidos. Por ello ponen cuidado en el número de cifras con que expresar el resultado de una medida con el propósito de incluir sólo aquellas que tienen algún significado experimental. Tales cifras reciben el nombre de cifras significativas. Una cifra es significativa cuando se conoce con una precisión aceptable. Así, cuando se mide con un termómetro que aprecia hasta 0,1 °C no tiene ningún sentido que se escriban resultados del tipo 36,25 °C o 22,175 °C, por ejemplo.

Todas las cifras que figuran en un resultado deben ser significativas. Este mismo criterio general debe respetarse cuando se opera con datos experimentales; es una cuestión de sentido común que por el simple hecho de operar con los números no es posible mejorar la precisión de los resultados si éstos tienen una base experimental. Cuando un resultado se escribe de modo que todas sus cifras sean significativas proporciona por sí mismo información sobre la precisión de la medida.

Cálculo de errores

Si las fuentes de error son únicamente de carácter aleatorio, es decir, si influyen unas veces por exceso y otras por defecto en el resultado de la medida, puede demostrarse que el valor que más se aproxima al verdadero valor es precisamente el valor medio. Ello es debido a que al promediar todos los resultados, los errores por exceso tenderán a compensarse con los errores por defecto y ello será tanto más cierto cuanto mayor sea el número de veces que se repita la medida. Por esta razón el procedimiento habitual para establecer un valor fiable de una cantidad M y de su incertidumbre correspondiente es el siguiente:

1) Repetir n veces la operación de medida de M y anotar los resultados M₁, M₂ … Mₙ

2) Calcular la media aritmética M de todos ellos:

3) Calcular la desviación media ΔM, es decir, la media aritmética de los valores absolutos de las desviaciones de los diferentes resultados de la medida respecto de su media M:

▫ El tomar los valores absolutos y no su signo equivale a situarse deliberadamente en la situación más desventajosa en la que los errores no se cancelan entre sí

5) Considerar ΔM como una cota o límite del error, de modo que el verdadero valor M de la magnitud medida estará comprendido entre los valores extremos M - ΔM y M + ΔM:

▫ M - ΔM < M < M + ΔM

6) Expresar el resultado en la forma:

▫ M ± ΔM

En ocasiones, si se trabaja con un número n de medidas elevado resulta útil disponer los resultados y sus errores ordenadamente en forma de tabla. En el ejemplo que sigue se recoge la medida del tiempo de caída de una bola realizada por un cronómetro que aprecia hasta la doble décima de segundo.

Empleo de cifras significativas

Para manejar correctamente los resultados expresados mediante cifras significativas es necesario seguir las siguientes reglas:

Cuando los ceros figuran como primeras cifras de un resultado no son considerados como cifras significativas, por ello el número de cifras significativas de un resultado es el mismo, cualquiera que sea la unidad en la que se exprese. Así, por ejemplo, si se desea expresar en metros el resultado de medir una longitud l de 3,2 cm con una regla que aprecie hasta el milímetro se tendrá:

I = 3,2 cm = 0,032 m

Y el resultado seguirá teniendo dos cifras significativas. Por esta razón se acostumbra a escribirlo recurriendo a las potencias de 10:

I = 3,2·10⁻² m

Cuando los ceros figuran como últimas cifras de números enteros, ello no implica que deban ser considerados, necesariamente, como cifras significativas. Así, por ejemplo, cuando se expresa la anterior cantidad en micras resulta I = 32.000 µ (1 µ = 1 milésima parte del mm = 10⁻³ mm); ello no quiere decir que el resultado tenga cinco cifras significativas, sino sólo dos en este caso. Para evitar este tipo de confusiones lo más apropiado es escribir el dato recurriendo, de nuevo, a las potencias de 10:

I = 3,2·10⁻⁵

Es posible preguntarse cómo arrastrar las cifras significativas en operaciones tales como la multiplicación o la división. Cuando se dispone de una calculadora electrónica parece como si se estuviera tentado a escribir los resultados con tantas cifras decimales como aparecen en pantalla, pero esto la mayoría de las veces carece de sentido. Valga como ejemplo el siguiente caso:

Se desea encontrar cuál es la superficie de una tira de papel. Se mide su longitud y su anchura utilizando una regla que aprecia hasta los milímetros y se obtiene 53,2 y 4,1 cm respectivamente. Multiplicando ambos resultados resulta:

S = 53,2·4,1 = 218,12 cm²

Pero ¿cuántas de estas cifras son verdaderamente significativas? La regla que sigue es la siguiente: el número de cifras significativas de un producto (o de un cociente) entre datos que corresponden a resultados de medidas no puede ser superior al de cualquiera de los factores. En el presente caso 4,1 tiene dos cifras significativas, luego el resultado en rigor se escribiría como:

S = 220 cm² = 22,10 cm²

Cuando como en este ejemplo es preciso redondear alguna cifra por no resultar significativa, se desprecia si es igual o interior a la mitad del valor de la unidad de la última cifra significativa y si es superior se considera ésta incrementada en una unidad. Dado que en el presente ejemplo 8 está por encima de la mitad de unidad de las decenas (10/2) se ha escrito el resultado como 220 cm² y no como 210 cm²

Autor: Kike González . México.

Editor: Ricardo Santiago Netto (Administrador de Fisicanet).

• ‹ Anterior
• Siguiente ›

¿Qué es un error relativo? ¿Cuál es el porcentaje de error?

• • Otros Temas
• Dónde estudiar
• Libro de visitas
• Entretenimiento-humor
• Acerca de Fisicanet
• Términos y condiciones
• Mapa del sitio

Éste sitio web usa cookies, si permanece aquí acepta su uso. Puede leer más sobre el uso de cookies en nuestra política de privacidad .