formulating the null and alternative hypothesis

• Mathematics
• Number System and Arithmetic
• Trigonometry
• Probability
• Mensuration
• Maths Formulas
• Integration Formulas
• Differentiation Formulas
• Trigonometry Formulas
• Algebra Formulas
• Mensuration Formula
• Statistics Formulas
• Trigonometric Table

Null Hypothesis

Null Hypothesis , often denoted as H 0, is a foundational concept in statistical hypothesis testing. It represents an assumption that no significant difference, effect, or relationship exists between variables within a population. It serves as a baseline assumption, positing no observed change or effect occurring. The null is t he truth or falsity of an idea in analysis.

In this article, we will discuss the null hypothesis in detail, along with some solved examples and questions on the null hypothesis.

Table of Content

What is Null Hypothesis?

Null hypothesis symbol, formula of null hypothesis, types of null hypothesis, null hypothesis examples, principle of null hypothesis, how do you find null hypothesis, null hypothesis in statistics, null hypothesis and alternative hypothesis, null hypothesis and alternative hypothesis examples, null hypothesis - practice problems.

Null Hypothesis in statistical analysis suggests the absence of statistical significance within a specific set of observed data. Hypothesis testing, using sample data, evaluates the validity of this hypothesis. Commonly denoted as H 0 or simply "null," it plays an important role in quantitative analysis, examining theories related to markets, investment strategies, or economies to determine their validity.

Null Hypothesis Meaning

Null Hypothesis represents a default position, often suggesting no effect or difference, against which researchers compare their experimental results. The Null Hypothesis, often denoted as H 0 asserts a default assumption in statistical analysis. It posits no significant difference or effect, serving as a baseline for comparison in hypothesis testing.

The null Hypothesis is represented as H 0 , the Null Hypothesis symbolizes the absence of a measurable effect or difference in the variables under examination.

Certainly, a simple example would be asserting that the mean score of a group is equal to a specified value like stating that the average IQ of a population is 100.

The Null Hypothesis is typically formulated as a statement of equality or absence of a specific parameter in the population being studied. It provides a clear and testable prediction for comparison with the alternative hypothesis. The formulation of the Null Hypothesis typically follows a concise structure, stating the equality or absence of a specific parameter in the population.

Mean Comparison (Two-sample t-test)

H 0 : μ 1 = μ 2

This asserts that there is no significant difference between the means of two populations or groups.

Proportion Comparison

H 0 : p 1 − p 2 = 0

This suggests no significant difference in proportions between two populations or conditions.

Equality in Variance (F-test in ANOVA)

H 0 : σ 1 = σ 2

This states that there's no significant difference in variances between groups or populations.

Independence (Chi-square Test of Independence):

H 0 : Variables are independent

This asserts that there's no association or relationship between categorical variables.

Null Hypotheses vary including simple and composite forms, each tailored to the complexity of the research question. Understanding these types is pivotal for effective hypothesis testing.

Equality Null Hypothesis (Simple Null Hypothesis)

The Equality Null Hypothesis, also known as the Simple Null Hypothesis, is a fundamental concept in statistical hypothesis testing that assumes no difference, effect or relationship between groups, conditions or populations being compared.

Non-Inferiority Null Hypothesis

In some studies, the focus might be on demonstrating that a new treatment or method is not significantly worse than the standard or existing one.

Superiority Null Hypothesis

The concept of a superiority null hypothesis comes into play when a study aims to demonstrate that a new treatment, method, or intervention is significantly better than an existing or standard one.

Independence Null Hypothesis

In certain statistical tests, such as chi-square tests for independence, the null hypothesis assumes no association or independence between categorical variables.

Homogeneity Null Hypothesis

In tests like ANOVA (Analysis of Variance), the null hypothesis suggests that there's no difference in population means across different groups.

• Medicine: Null Hypothesis: "No significant difference exists in blood pressure levels between patients given the experimental drug versus those given a placebo."
• Education: Null Hypothesis: "There's no significant variation in test scores between students using a new teaching method and those using traditional teaching."
• Economics: Null Hypothesis: "There's no significant change in consumer spending pre- and post-implementation of a new taxation policy."
• Environmental Science: Null Hypothesis: "There's no substantial difference in pollution levels before and after a water treatment plant's establishment."

The principle of the null hypothesis is a fundamental concept in statistical hypothesis testing. It involves making an assumption about the population parameter or the absence of an effect or relationship between variables.

In essence, the null hypothesis (H 0 ) proposes that there is no significant difference, effect, or relationship between variables. It serves as a starting point or a default assumption that there is no real change, no effect or no difference between groups or conditions.

The null hypothesis is usually formulated to be tested against an alternative hypothesis (H 1 or H \alpha ) which suggests that there is an effect, difference or relationship present in the population.

Null Hypothesis Rejection

Rejecting the Null Hypothesis occurs when statistical evidence suggests a significant departure from the assumed baseline. It implies that there is enough evidence to support the alternative hypothesis, indicating a meaningful effect or difference. Null Hypothesis rejection occurs when statistical evidence suggests a deviation from the assumed baseline, prompting a reconsideration of the initial hypothesis.

Identifying the Null Hypothesis involves defining the status quotient, asserting no effect and formulating a statement suitable for statistical analysis.

When is Null Hypothesis Rejected?

The Null Hypothesis is rejected when statistical tests indicate a significant departure from the expected outcome, leading to the consideration of alternative hypotheses. It occurs when statistical evidence suggests a deviation from the assumed baseline, prompting a reconsideration of the initial hypothesis.

In statistical hypothesis testing, researchers begin by stating the null hypothesis, often based on theoretical considerations or previous research. The null hypothesis is then tested against an alternative hypothesis (Ha), which represents the researcher's claim or the hypothesis they seek to support.

The process of hypothesis testing involves collecting sample data and using statistical methods to assess the likelihood of observing the data if the null hypothesis were true. This assessment is typically done by calculating a test statistic, which measures the difference between the observed data and what would be expected under the null hypothesis.

In the realm of hypothesis testing, the null hypothesis (H 0 ) and alternative hypothesis (H₁ or Ha) play critical roles. The null hypothesis generally assumes no difference, effect, or relationship between variables, suggesting that any observed change or effect is due to random chance. Its counterpart, the alternative hypothesis, asserts the presence of a significant difference, effect, or relationship between variables, challenging the null hypothesis. These hypotheses are formulated based on the research question and guide statistical analyses.

Difference Between Null Hypothesis and Alternative Hypothesis

The null hypothesis (H 0 ) serves as the baseline assumption in statistical testing, suggesting no significant effect, relationship, or difference within the data. It often proposes that any observed change or correlation is merely due to chance or random variation. Conversely, the alternative hypothesis (H 1 or Ha) contradicts the null hypothesis, positing the existence of a genuine effect, relationship or difference in the data. It represents the researcher's intended focus, seeking to provide evidence against the null hypothesis and support for a specific outcome or theory. These hypotheses form the crux of hypothesis testing, guiding the assessment of data to draw conclusions about the population being studied.

Let's envision a scenario where a researcher aims to examine the impact of a new medication on reducing blood pressure among patients. In this context:

Null Hypothesis (H 0 ): "The new medication does not produce a significant effect in reducing blood pressure levels among patients."

Alternative Hypothesis (H 1 or Ha): "The new medication yields a significant effect in reducing blood pressure levels among patients."

The null hypothesis implies that any observed alterations in blood pressure subsequent to the medication's administration are a result of random fluctuations rather than a consequence of the medication itself. Conversely, the alternative hypothesis contends that the medication does indeed generate a meaningful alteration in blood pressure levels, distinct from what might naturally occur or by random chance.

People Also Read:

Mathematics Maths Formulas Probability and Statistics

Example 1: A researcher claims that the average time students spend on homework is 2 hours per night.

Null Hypothesis (H 0 ): The average time students spend on homework is equal to 2 hours per night. Data: A random sample of 30 students has an average homework time of 1.8 hours with a standard deviation of 0.5 hours. Test Statistic and Decision: Using a t-test, if the calculated t-statistic falls within the acceptance region, we fail to reject the null hypothesis. If it falls in the rejection region, we reject the null hypothesis. Conclusion: Based on the statistical analysis, we fail to reject the null hypothesis, suggesting that there is not enough evidence to dispute the claim of the average homework time being 2 hours per night.

Example 2: A company asserts that the error rate in its production process is less than 1%.

Null Hypothesis (H 0 ): The error rate in the production process is 1% or higher. Data: A sample of 500 products shows an error rate of 0.8%. Test Statistic and Decision: Using a z-test, if the calculated z-statistic falls within the acceptance region, we fail to reject the null hypothesis. If it falls in the rejection region, we reject the null hypothesis. Conclusion: The statistical analysis supports rejecting the null hypothesis, indicating that there is enough evidence to dispute the company's claim of an error rate of 1% or higher.

Q1. A researcher claims that the average time spent by students on homework is less than 2 hours per day. Formulate the null hypothesis for this claim?

Q2. A manufacturing company states that their new machine produces widgets with a defect rate of less than 5%. Write the null hypothesis to test this claim?

Q3. An educational institute believes that their online course completion rate is at least 60%. Develop the null hypothesis to validate this assertion?

Q4. A restaurant claims that the waiting time for customers during peak hours is not more than 15 minutes. Formulate the null hypothesis for this claim?

Q5. A study suggests that the mean weight loss after following a specific diet plan for a month is more than 8 pounds. Construct the null hypothesis to evaluate this statement?

Summary - Null Hypothesis and Alternative Hypothesis

The null hypothesis (H 0 ) and alternative hypothesis (H a ) are fundamental concepts in statistical hypothesis testing. The null hypothesis represents the default assumption, stating that there is no significant effect, difference, or relationship between variables. It serves as the baseline against which the alternative hypothesis is tested. In contrast, the alternative hypothesis represents the researcher's hypothesis or the claim to be tested, suggesting that there is a significant effect, difference, or relationship between variables. The relationship between the null and alternative hypotheses is such that they are complementary, and statistical tests are conducted to determine whether the evidence from the data is strong enough to reject the null hypothesis in favor of the alternative hypothesis. This decision is based on the strength of the evidence and the chosen level of significance. Ultimately, the choice between the null and alternative hypotheses depends on the specific research question and the direction of the effect being investigated.

FAQs on Null Hypothesis

What does null hypothesis stands for.

The null hypothesis, denoted as H 0 ​, is a fundamental concept in statistics used for hypothesis testing. It represents the statement that there is no effect or no difference, and it is the hypothesis that the researcher typically aims to provide evidence against.

How to Form a Null Hypothesis?

A null hypothesis is formed based on the assumption that there is no significant difference or effect between the groups being compared or no association between variables being tested. It often involves stating that there is no relationship, no change, or no effect in the population being studied.

When Do we reject the Null Hypothesis?

In statistical hypothesis testing, if the p-value (the probability of obtaining the observed results) is lower than the chosen significance level (commonly 0.05), we reject the null hypothesis. This suggests that the data provides enough evidence to refute the assumption made in the null hypothesis.

What is a Null Hypothesis in Research?

In research, the null hypothesis represents the default assumption or position that there is no significant difference or effect. Researchers often try to test this hypothesis by collecting data and performing statistical analyses to see if the observed results contradict the assumption.

What Are Alternative and Null Hypotheses?

The null hypothesis (H0) is the default assumption that there is no significant difference or effect. The alternative hypothesis (H1 or Ha) is the opposite, suggesting there is a significant difference, effect or relationship.

What Does it Mean to Reject the Null Hypothesis?

Rejecting the null hypothesis implies that there is enough evidence in the data to support the alternative hypothesis. In simpler terms, it suggests that there might be a significant difference, effect or relationship between the groups or variables being studied.

How to Find Null Hypothesis?

Formulating a null hypothesis often involves considering the research question and assuming that no difference or effect exists. It should be a statement that can be tested through data collection and statistical analysis, typically stating no relationship or no change between variables or groups.

How is Null Hypothesis denoted?

The null hypothesis is commonly symbolized as H 0 in statistical notation.

What is the Purpose of the Null hypothesis in Statistical Analysis?

The null hypothesis serves as a starting point for hypothesis testing, enabling researchers to assess if there's enough evidence to reject it in favor of an alternative hypothesis.

What happens if we Reject the Null hypothesis?

Rejecting the null hypothesis implies that there is sufficient evidence to support an alternative hypothesis, suggesting a significant effect or relationship between variables.

What are Test for Null Hypothesis?

Various statistical tests, such as t-tests or chi-square tests, are employed to evaluate the validity of the Null Hypothesis in different scenarios.

Similar Reads

• Null Hypothesis Null Hypothesis, often denoted as H0, is a foundational concept in statistical hypothesis testing. It represents an assumption that no significant difference, effect, or relationship exists between variables within a population. It serves as a baseline assumption, positing no observed change or effe 12 min read
• Hypothesis Testing Formula Statistics is a discipline of applied mathematics that deals with gathering, describing, analyzing, and inferring conclusions from numerical data. Differential and integral calculus, linear algebra, and probability theory are all used substantially in statistics' mathematical theories. Statisticians 8 min read
• SQL IS NULL SQL IS NULL is a logical operator that checks for NULL values in a column. IS NULL Operator in SQLIS NULL Operator in SQL is used to test for empty or missing values in a column. It checks if the specified expression evaluates to NULL, if it evaluates to NULL, it returns TRUE; otherwise, it returns 3 min read
• SQLite IS NULL SQLite is a server-less database engine and it is written in c programming language. It is developed by D. Richard Hipp in the year 2000. The main moto for developing the SQLite is to escape from using the complex database engines like MYSQL.etc. It has become one of the most popular database engine 6 min read
• MySQL NOT NULL Constraint In the database management system maintaining data reliability and data accuracy is very important. MySQL is a popular relational database management system, which offers various constraints to provide security and ensure the integrity of the stored data. There are various key constraints present in 4 min read
• Permutation Hypothesis Test in R Programming In simple words, the permutation hypothesis test in R is a way of comparing a numerical value of 2 groups. The permutation Hypothesis test is an alternative to: Independent two-sample t-test Mann-Whitney U aka Wilcoxon Rank-Sum Test Let's implement this test in R programming. Why use the Permutation 6 min read
• Null in JavaScript In JavaScript, `null` indicates the deliberate absence of any object value. It's a primitive value that denotes the absence of a value or serves as a placeholder for an object that isn't present. `null` differs from `undefined`, which signifies a variable that has been declared but hasn't been assig 3 min read
• What is Null Session? The null session attack has been present since Windows 2000 was extensively used; yet, system administrators do not take this type of attack into account when implementing network security measures. This can have unimaginable consequences since hackers can use this type of attack to obtain all of th 4 min read
• How to Use the linearHypothesis() Function in R In statistics, understanding how variables relate to each other is crucial. This helps in making smart decisions. When we build regression models, we need to check if certain combinations of variables are statistically significant. In R Programming Language a tool called linear hypothesis () in the 4 min read
• What is /Dev/Null in Linux? If you have been learning shell programming, you may already have come across something like /dev/null. In this article, we will understand what it is and how it is used. Let's start off by understanding what /dev is. What is /dev?In the Linux file system, everything is a file or a directory. Even d 5 min read
• MySQL Handling NULL Values In MySQL, NULL values represent the absence of data or a missing value. Understanding how to handle NULL values is crucial for effective database management and querying. This article will cover various aspects of working with NULL how to handle them in queries, update statements, and table definiti 4 min read
• SQLite NOT NULL Constraint SQLite is a very lightweight and embedded Relational Database Management System (RDBMS). It requires very minimal configuration and it is self-contained. It is serverless, therefore it is a perfect fit for mobile applications, simple desktop applications, and embedded systems. While it may not be a 4 min read
• Why hypothesis testing is important in research ? Hypothesis Testing allows researchers to evaluate the validity of their assumptions and draw conclusions based on evidence. It provides a framework for making predictions and determining whether observed results are statistically significant or just occurred by chance. By applying various statistica 6 min read
• How to use Is Not Null in PySpark In data processing, handling null values is a crucial task to ensure the accuracy and reliability of the analysis. PySpark, the Python API for Apache Spark, provides powerful methods to handle null values efficiently. In this article, we will go through how to use the isNotNull method in PySpark to 4 min read
• MySQL IS NULL Operator The IS NULL operator in MySQL is a powerful tool for handling records with missing or incomplete data. It enables precise querying and data management by allowing users to identify and act upon fields where values are absent. In this article, We will learn about the MySQL IS NULL Operator by underst 3 min read
• Null Space of a Matrix Null space of a matrix is a fundamental concept in linear algebra that describes the set of all possible solutions to the equation Ax = 0, where A is a matrix and x is a vector. This space consists of vectors that, when multiplied by the matrix A, result in the zero vector. In simpler terms, if you 6 min read
• MariaDB Not Null Constraint MariaDB is an open-source relational database management system. In a relational database, data integrity is very important. So, we use the NOT NULL constraint to ensure the data integrity in a table within a database. So, In this article, we are going to discuss how a NOT NULL constraint helps to m 4 min read
• Testing Various Hypothesis Test for Coefficients in R Hypothesis testing plays a critical role in statistical modeling, helping us assess whether the independent variables (predictors) in a model significantly impact the dependent variable (outcome). In the context of regression analysis, testing the coefficients allows us to evaluate the significance 5 min read
• NULL Pointer in C++ A NULL Pointer in C++ indicates the absence of a valid memory address in C++. It tells that the pointer is not pointing to any valid memory location In other words, it has the value "NULL" (or 'nullptr' since C++11). This is generally done at the time of variable declaration to check whether the poi 4 min read
• Geeks Premier League
• School Learning
• Geeks Premier League 2023
• Math-Concepts

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Interested in teaching this course?

Lumen can help! Review our up-to-date Introduction to Statistics by clicking the link below. From there, you can request a demo and review the course materials in your Learning Management System (LMS).

Module 9: Hypothesis Testing With One Sample

Null and alternative hypotheses, learning outcomes.

• Describe hypothesis testing in general and in practice

The actual test begins by considering two  hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 : The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.

H a : The alternative hypothesis : It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make adecision. There are two options for a  decision . They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in  H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30

H a : More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

H 0 : The drug reduces cholesterol by 25%. p = 0.25

H a : The drug does not reduce cholesterol by 25%. p ≠ 0.25

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

H 0 : μ = 2.0

H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 66 H a : μ __ 66

• H 0 : μ = 66
• H a : μ ≠ 66

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

H 0 : μ ≥ 5

H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 45 H a : μ __ 45

• H 0 : μ ≥ 45
• H a : μ < 45

In an issue of U.S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

H 0 : p ≤ 0.066

H a : p > 0.066

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : p __ 0.40 H a : p __ 0.40

• H 0 : p = 0.40
• H a : p > 0.40

Concept Review

In a  hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis , typically denoted with H 0 . The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality (=, ≤ or ≥) Always write the alternative hypothesis , typically denoted with H a or H 1 , using less than, greater than, or not equals symbols, i.e., (≠, >, or <). If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis. Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.

Formula Review

H 0 and H a are contradictory.

Candela Citations

• OpenStax, Statistics, Null and Alternative Hypotheses. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:58/Introductory_Statistics . License : CC BY: Attribution
• Introductory Statistics . Authored by : Barbara Illowski, Susan Dean. Provided by : Open Stax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
• Simple hypothesis testing | Probability and Statistics | Khan Academy. Authored by : Khan Academy. Located at : https://youtu.be/5D1gV37bKXY . License : All Rights Reserved . License Terms : Standard YouTube License

• The Open University
• Accessibility hub
• Guest user / Sign out
• Study with The Open University

My OpenLearn Profile

Personalise your OpenLearn profile, save your favourite content and get recognition for your learning

About this free course

Become an ou student, download this course, share this free course.

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

1.1 Formulating null and alternative hypotheses

In the world of scientific inquiry, you often begin with a null hypothesis (H 0 ), which expresses the currently accepted value for a parameter in the population. The alternative hypothesis (H a ), on the other hand, is the opposite of the null hypothesis and challenges the currently accepted value.

To illustrate this concept of null and alternative hypotheses, you will look at some well-known stories and examples.

In ancient and medieval times, the widely held belief was that all planets orbited around the Earth, as the Earth was considered the centre of the universe. This idea can be considered the null hypothesis, as it represents the currently accepted value for a parameter in the population. Thus, it can be written as:

H 0 : All planets orbit around the Earth.

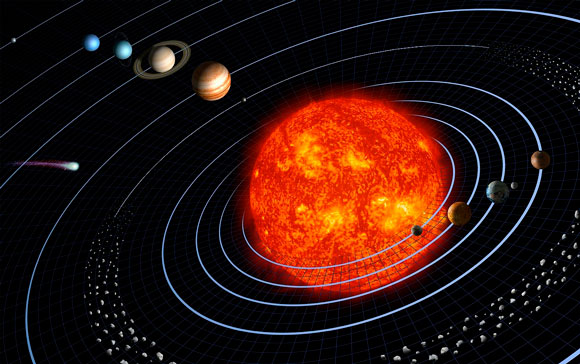
Planets revolving around the Sun

In the world of business and finance, the idea that paper money must be backed by gold (the gold standard) was also a commonly held belief for a long time. This belief can be considered a null hypothesis. However, following the Great Depression, people began to question this belief and broke the link between banknotes and gold. This alternative hypothesis challenged the gold standard, and it eventually became widely accepted that the value of paper money is not necessarily equal to a fixed amount of gold. Thus, H 0 and H a statements can be written as:

H 0 : The value of paper money is equal to a fixed amount of gold.

H a : The value of paper money is not equal to a fixed amount of gold.

In modern times, people generally place their trust in the value of banknotes issued by central banks or monetary authorities, which are backed by a strong government. This belief can be considered a null hypothesis. However, digital currency, such as Bitcoin, has emerged as an alternative to traditional paper money. Bitcoin is not backed by any central bank or monetary authority, and transactions involving Bitcoin are verified by network nodes using cryptography and recorded in a blockchain. This alternative hypothesis challenges the belief that the value of paper money is solely based on people's trust in central banks or monetary authorities. Thus, H 0 and H a statements can be written as:

H 0 : The value of paper money is equal to people’s trust in central banks or monetary authorities.

H a : The value of paper money is not equal to people’s trust in central banks or monetary authorities.

In conclusion, the alternative hypothesis always challenges the idea expressed in the null hypothesis. By testing the null hypothesis against the alternative hypothesis, you can determine which idea is more supported by the available data. The alternative hypothesis is often referred to as a ‘research hypothesis’ because it initiates the motivation and opportunities for further research.

Let’s return to the first example given in Section 1. If you see that your friends and relatives make more or less than £26,000 annually on average, perhaps you should question the widely accepted proposition of £26,000 as the average annual salary in the UK. This will enable you to develop an alternative hypothesis:

H a : Average annual salary in the UK is not equal to £26,000.

The following activity will test your knowledge of null and alternative hypotheses.

Activity 1 Null hypothesis versus alternative hypothesis

Read the following statements. Can you develop a null hypothesis and an alternative hypothesis?

‘It is believed that a high-end coffee machine produces a cup of caffè latte with an average of 1 cm of foam. The hotel employee claims that after the machine has been repaired, it is no longer able to produce a cup of caffè latte with 1cm foam.’

H 0 : a coffee machine makes a cup of caffè latte with 1cm foam on average.

H a : a coffee machine cannot make a cup of caffè latte with 1 cm foam on average.

If you have developed the hypotheses H 0 and H a as mentioned in the discussion to Activity 1, you have shown that you are familiar with the structure of different types of hypotheses. However, in the next section you will explore the concept of hypothesis formulation further.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

5.2 - writing hypotheses.

The first step in conducting a hypothesis test is to write the hypothesis statements that are going to be tested. For each test you will have a null hypothesis (\(H_0\)) and an alternative hypothesis (\(H_a\)).

When writing hypotheses there are three things that we need to know: (1) the parameter that we are testing (2) the direction of the test (non-directional, right-tailed or left-tailed), and (3) the value of the hypothesized parameter.

• At this point we can write hypotheses for a single mean (\(\mu\)), paired means(\(\mu_d\)), a single proportion (\(p\)), the difference between two independent means (\(\mu_1-\mu_2\)), the difference between two proportions (\(p_1-p_2\)), a simple linear regression slope (\(\beta\)), and a correlation (\(\rho\)). 
• The research question will give us the information necessary to determine if the test is two-tailed (e.g., "different from," "not equal to"), right-tailed (e.g., "greater than," "more than"), or left-tailed (e.g., "less than," "fewer than").
• The research question will also give us the hypothesized parameter value. This is the number that goes in the hypothesis statements (i.e., \(\mu_0\) and \(p_0\)). For the difference between two groups, regression, and correlation, this value is typically 0.

Hypotheses are always written in terms of population parameters (e.g., \(p\) and \(\mu\)).  The tables below display all of the possible hypotheses for the parameters that we have learned thus far. Note that the null hypothesis always includes the equality (i.e., =).

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Hypothesis Testing with One Sample

Null and Alternative Hypotheses

OpenStaxCollege

[latexpage]

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 : The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.

H a : The alternative hypothesis: It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

H 0 : The drug reduces cholesterol by 25%. p = 0.25

H a : The drug does not reduce cholesterol by 25%. p ≠ 0.25

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

H 0 : μ = 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ = 66
• H a : μ ≠ 66

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

H 0 : μ ≥ 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ ≥ 45
• H a : μ < 45

In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

H 0 : p ≤ 0.066

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : p = 0.40
• H a : p > 0.40

<!– ??? –>

Bring to class a newspaper, some news magazines, and some Internet articles . In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

Chapter Review

In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we:

Formula Review

H 0 and H a are contradictory.

If α ≤ p -value, then do not reject H 0 .

If α > p -value, then reject H 0 .

α is preconceived. Its value is set before the hypothesis test starts. The p -value is calculated from the data.

You are testing that the mean speed of your cable Internet connection is more than three Megabits per second. What is the random variable? Describe in words.

The random variable is the mean Internet speed in Megabits per second.

You are testing that the mean speed of your cable Internet connection is more than three Megabits per second. State the null and alternative hypotheses.

The American family has an average of two children. What is the random variable? Describe in words.

The random variable is the mean number of children an American family has.

The mean entry level salary of an employee at a company is 💲58,000. You believe it is higher for IT professionals in the company. State the null and alternative hypotheses.

A sociologist claims the probability that a person picked at random in Times Square in New York City is visiting the area is 0.83. You want to test to see if the proportion is actually less. What is the random variable? Describe in words.

The random variable is the proportion of people picked at random in Times Square visiting the city.

A sociologist claims the probability that a person picked at random in Times Square in New York City is visiting the area is 0.83. You want to test to see if the claim is correct. State the null and alternative hypotheses.

In a population of fish, approximately 42% are female. A test is conducted to see if, in fact, the proportion is less. State the null and alternative hypotheses.

Suppose that a recent article stated that the mean time spent in jail by a first–time convicted burglar is 2.5 years. A study was then done to see if the mean time has increased in the new century. A random sample of 26 first-time convicted burglars in a recent year was picked. The mean length of time in jail from the survey was 3 years with a standard deviation of 1.8 years. Suppose that it is somehow known that the population standard deviation is 1.5. If you were conducting a hypothesis test to determine if the mean length of jail time has increased, what would the null and alternative hypotheses be? The distribution of the population is normal.

A random survey of 75 death row inmates revealed that the mean length of time on death row is 17.4 years with a standard deviation of 6.3 years. If you were conducting a hypothesis test to determine if the population mean time on death row could likely be 15 years, what would the null and alternative hypotheses be?

• H 0 : __________
• H a : __________
• H 0 : μ = 15
• H a : μ ≠ 15

The National Institute of Mental Health published an article stating that in any one-year period, approximately 9.5 percent of American adults suffer from depression or a depressive illness. Suppose that in a survey of 100 people in a certain town, seven of them suffered from depression or a depressive illness. If you were conducting a hypothesis test to determine if the true proportion of people in that town suffering from depression or a depressive illness is lower than the percent in the general adult American population, what would the null and alternative hypotheses be?

Some of the following statements refer to the null hypothesis, some to the alternate hypothesis.

State the null hypothesis, H 0 , and the alternative hypothesis. H a , in terms of the appropriate parameter ( μ or p ).

• The mean number of years Americans work before retiring is 34.
• At most 60% of Americans vote in presidential elections.
• The mean starting salary for San Jose State University graduates is at least 💲100,000 per year.
• Twenty-nine percent of high school seniors get drunk each month.
• Fewer than 5% of adults ride the bus to work in Los Angeles.
• The mean number of cars a person owns in her lifetime is not more than ten.
• About half of Americans prefer to live away from cities, given the choice.
• Europeans have a mean paid vacation each year of six weeks.
• The chance of developing breast cancer is under 11% for women.
• Private universities’ mean tuition cost is more than 💲20,000 per year.
• H 0 : μ = 34; H a : μ ≠ 34
• H 0 : p ≤ 0.60; H a : p > 0.60
• H 0 : μ ≥ 100,000; H a : μ < 100,000
• H 0 : p = 0.29; H a : p ≠ 0.29
• H 0 : p = 0.05; H a : p < 0.05
• H 0 : μ ≤ 10; H a : μ > 10
• H 0 : p = 0.50; H a : p ≠ 0.50
• H 0 : μ = 6; H a : μ ≠ 6
• H 0 : p ≥ 0.11; H a : p < 0.11
• H 0 : μ ≤ 20,000; H a : μ > 20,000

Over the past few decades, public health officials have examined the link between weight concerns and teen girls’ smoking. Researchers surveyed a group of 273 randomly selected teen girls living in Massachusetts (between 12 and 15 years old). After four years the girls were surveyed again. Sixty-three said they smoked to stay thin. Is there good evidence that more than thirty percent of the teen girls smoke to stay thin? The alternative hypothesis is:

• p < 0.30
• p > 0.30

A statistics instructor believes that fewer than 20% of Evergreen Valley College (EVC) students attended the opening night midnight showing of the latest Harry Potter movie. She surveys 84 of her students and finds that 11 attended the midnight showing. An appropriate alternative hypothesis is:

• p > 0.20
• p < 0.20

Previously, an organization reported that teenagers spent 4.5 hours per week, on average, on the phone. The organization thinks that, currently, the mean is higher. Fifteen randomly chosen teenagers were asked how many hours per week they spend on the phone. The sample mean was 4.75 hours with a sample standard deviation of 2.0. Conduct a hypothesis test. The null and alternative hypotheses are:

• H o : \(\overline{x}\) = 4.5, H a : \(\overline{x}\) > 4.5
• H o : μ ≥ 4.5, H a : μ < 4.5
• H o : μ = 4.75, H a : μ > 4.75
• H o : μ = 4.5, H a : μ > 4.5

Data from the National Institute of Mental Health. Available online at http://www.nimh.nih.gov/publicat/depression.cfm.

Null and Alternative Hypotheses Copyright © 2013 by OpenStaxCollege is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Hypothesis Testing: Null Hypothesis and Alternative Hypothesis

Join over 2 million students who advanced their careers with 365 Data Science. Learn from instructors who have worked at Meta, Spotify, Google, IKEA, Netflix, and Coca-Cola and master Python, SQL, Excel, machine learning, data analysis, AI fundamentals, and more.

Figuring out exactly what the null hypothesis and the alternative hypotheses are is not a walk in the park. Hypothesis testing is based on the knowledge that you can acquire by going over what we have previously covered about statistics in our blog.

So, if you don’t want to have a hard time keeping up, make sure you have read all the tutorials about confidence intervals , distributions , z-tables and t-tables .

We've also made a video on null hypothesis vs alternative hypothesis - you can watch it below or just scroll down if you prefer reading.

Confidence intervals provide us with an estimation of where the parameters are located. You can obtain them with our confidence interval calculator and learn more about them in the related article.

However, when we are making a decision, we need a yes or no answer. The correct approach, in this case, is to use a test .

Here we will start learning about one of the fundamental tasks in statistics - hypothesis testing !

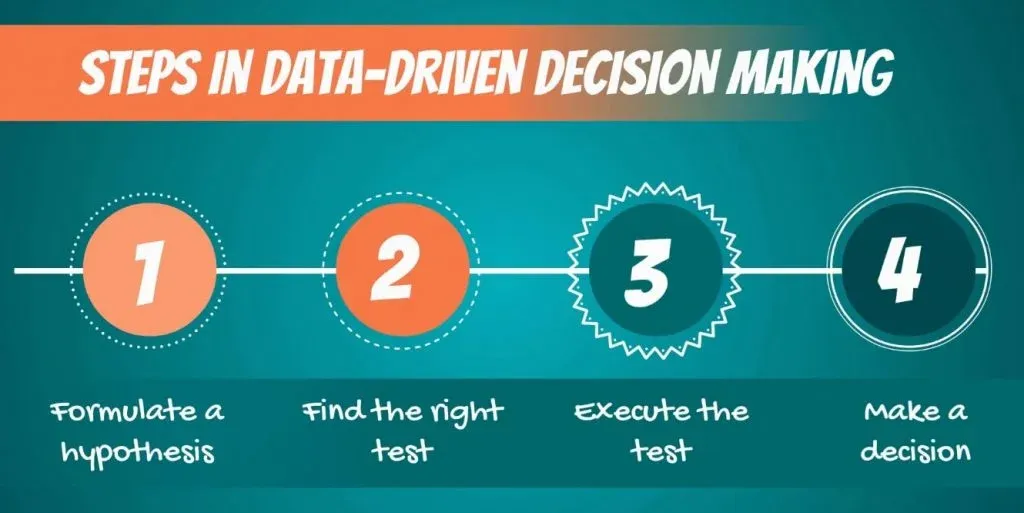
The Hypothesis Testing Process

  First off, let’s talk about data-driven decision-making. It consists of the following steps:

• First, we must formulate a hypothesis .
• After doing that, we have to find the right test for our hypothesis .
• Then, we execute the test.
• Finally, we make a decision based on the result.

Let’s start from the beginning.

What is a Hypothesis?

Though there are many ways to define it, the most intuitive must be:

“A hypothesis is an idea that can be tested.”

This is not the formal definition, but it explains the point very well.

So, if we say that apples in New York are expensive, this is an idea or a statement. However, it is not testable, until we have something to compare it with.

For instance, if we define expensive as: any price higher than $1.75 dollars per pound, then it immediately becomes a hypothesis .

What Cannot Be a Hypothesis?

An example may be: would the USA do better or worse under a Clinton administration, compared to a Trump administration? Statistically speaking, this is an idea , but there is no data to test it. Therefore, it cannot be a hypothesis of a statistical test.

Actually, it is more likely to be a topic of another discipline.

Conversely, in statistics, we may compare different US presidencies that have already been completed. For example, the Obama administration and the Bush administration, as we have data on both.

A Two-Sided Test

Alright, let’s get out of politics and get into hypotheses . Here’s a simple topic that CAN be tested.

According to Glassdoor (the popular salary information website), the mean data scientist salary in the US is 113,000 dollars.

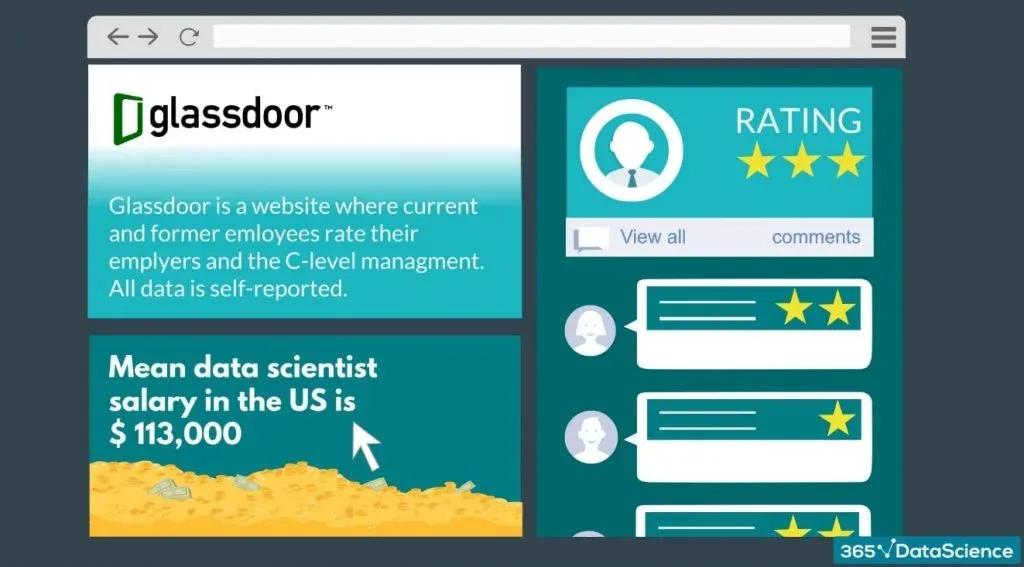
So, we want to test if their estimate is correct.

The Null and Alternative Hypotheses

There are two hypotheses that are made: the null hypothesis , denoted H 0 , and the alternative hypothesis , denoted H 1 or H A .

The null hypothesis is the one to be tested and the alternative is everything else. In our example:

The null hypothesis would be: The mean data scientist salary is 113,000 dollars.

While the alternative : The mean data scientist salary is not 113,000 dollars.

Author's note: If you're interested in a data scientist career, check out our articles Data Scientist Career Path , 5 Business Basics for Data Scientists , Data Science Interview Questions , and 15 Data Science Consulting Companies Hiring Now .

An Example of a One-Sided Test

You can also form one-sided or one-tailed tests.

Say your friend, Paul, told you that he thinks data scientists earn more than 125,000 dollars per year. You doubt him, so you design a test to see who’s right.

The null hypothesis of this test would be: The mean data scientist salary is more than 125,000 dollars.

The alternative will cover everything else, thus: The mean data scientist salary is less than or equal to 125,000 dollars.

Important: The outcomes of tests refer to the population parameter rather than the sample statistic! So, the result that we get is for the population.

Important: Another crucial consideration is that, generally, the researcher is trying to reject the null hypothesis . Think about the null hypothesis as the status quo and the alternative as the change or innovation that challenges that status quo. In our example, Paul was representing the status quo, which we were challenging.

Let’s go over it once more. In statistics, the null hypothesis is the statement we are trying to reject. Therefore, the null hypothesis is the present state of affairs, while the alternative is our personal opinion.

Why Hypothesis Testing Works

Right now, you may be feeling a little puzzled. This is normal because this whole concept is counter-intuitive at the beginning. However, there is an extremely easy way to continue your journey of exploring it. By diving into the linked tutorial, you will find out why hypothesis testing actually works.

Interested in learning more? You can take your skills from good to great with our statistics course!

Try statistics course for free

Next Tutorial:  Hypothesis Testing: Significance Level and Rejection Region

Iliya Valchanov

Co-founder of 365 Data Science

Iliya is a finance graduate with a strong quantitative background who chose the exciting path of a startup entrepreneur. He demonstrated a formidable affinity for numbers during his childhood, winning more than 90 national and international awards and competitions through the years. Iliya started teaching at university, helping other students learn statistics and econometrics. Inspired by his first happy students, he co-founded 365 Data Science to continue spreading knowledge. He authored several of the program’s online courses in mathematics, statistics, machine learning, and deep learning.

We Think you'll also like

Statistics Tutorials

False Positive vs. False Negative: Type I and Type II Errors in Statistical Hypothesis Testing

Hypothesis Testing with Z-Test: Significance Level and Rejection Region

Calculating and Using Covariance and Linear Correlation Coefficient

Visualizing Data with Bar, Pie and Pareto Charts

9.1 Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 : The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.

H a : The alternative hypothesis: It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 . This is usually what the researcher is trying to prove.

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are "reject H 0 " if the sample information favors the alternative hypothesis or "do not reject H 0 " or "decline to reject H 0 " if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example 9.1

H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ .30 H a : More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

Example 9.2

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are: H 0 : μ = 2.0 H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 66
• H a : μ __ 66

Example 9.3

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are: H 0 : μ ≥ 5 H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 45
• H a : μ __ 45

Example 9.4

In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : p __ 0.40
• H a : p __ 0.40

Collaborative Exercise

Bring to class a newspaper, some news magazines, and some Internet articles . In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/introductory-statistics-2e/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Introductory Statistics 2e
• Publication date: Dec 13, 2023
• Location: Houston, Texas
• Book URL: https://openstax.org/books/introductory-statistics-2e/pages/1-introduction
• Section URL: https://openstax.org/books/introductory-statistics-2e/pages/9-1-null-and-alternative-hypotheses

© Jul 18, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.